

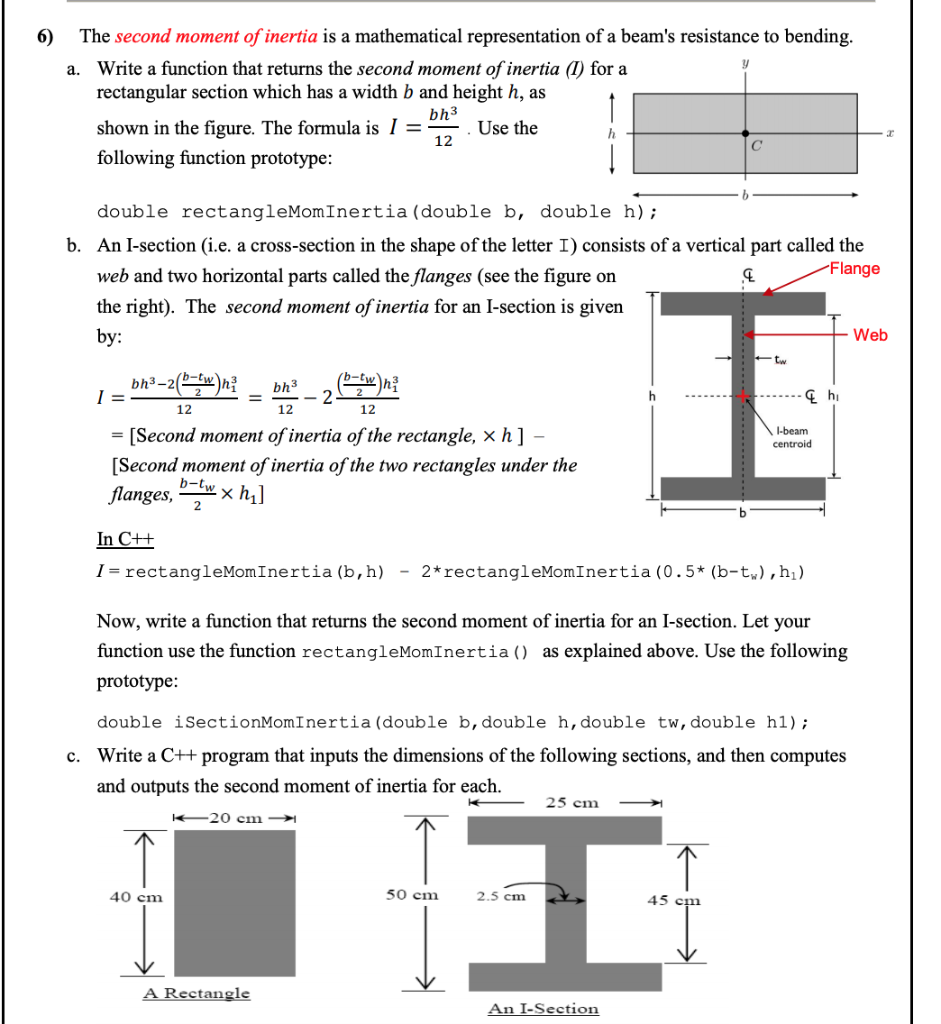
The moment of an large area about any axis is equal to the algebraic sum of the moments of its component areas. This is done in the same way that the center of gravity can be found by taking moments of weights. The centroid of any area can be found by taking moments of identifiable areas (such as rectangles or triangles) about any axis. The exact location of the centroid can be determined as described above, with graphic statics, or numerically. This is not a problem since the centroid is really only used as a reference point from which one measures distances. Hollow pipes, L shaped and some irregular shaped sections all have thir centroid located outside of the material of the section. The centroid of a section is not always within the area or material of the section. The circle has an infinite number of lines of symmetry and the square has four. One knows that the centroid of a circle is at its center and that of a square is at the intersection of two lines drawn connecting the midpoints of the parallel sides. The position of the center of gravity for some simple shapes is easily determined by inspection. This might seem obvious, but the concept of the centroid is very important to understand both graphically and numerically. This means that if it were required to balance the area (or body or section) in a horizontal position by placing a nail underneath it, the point of the nail would best be placed directly below the point where the lines of symmetry meet. Thus, the centroid is at the point where the lines intersect. If a body (or area or section) has two (or more) lines of symmetry, the centroid must lie somewhere along each of the lines. This means that if it were required to balance the area (or body or section) in a horizontal position by placing a pencil or edge underneath it, the pencil would be best laid directly under the line of symmetry. If the area (or section or body) has one line of symmetry, the centroid will lie somewhere along the line of symmetry. Symmetry can be very useful to help determine the location of the centroid of an area. It is often useful for the centroid of the area to be determined in either case. The planar surface (or figure) may represent an actual area (like a tributary floor area or the cross-section of a beam) or a figurative diagram (like a load or a bending moment diagram). The centroid of a two dimensional surface (such as the cross-section of a structural shape) is a point that corresponds to the center of gravity of a very thin homogeneous plate of the same area and shape. The Beams Shown are a Wood and Steel Beams We will limit our application of the Moment of Inertia as it applies to Structural Components identified here. The farther out the object's mass is, the more rotational inertia the object has, and the more force is required to change its rotation rate. Therefore, it encompasses not just how much mass the object has overall, but how far each bit of mass is from the axis. The moment of inertia of an object about a given axis describes how difficult it is to change its angular motion about that axis. The symbol I and sometimes J are usually used to refer to the moment of inertia or polar moment of inertia. The moment of inertia plays much the same role in rotational dynamics as mass does in linear dynamics, describing the relationship between angular momentum and angular velocity, torque and angular acceleration, and several other quantities. It is the inertia of a rotating body with respect to its rotation.
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, (SI units kg m 2) is a measure of an object's resistance to changes to its rotation. In other circumstances however this is not accepteble.(Moment of Inertia - TotalConstructionHelp) It is rather acceptable to ignore the centroidal term for the flange of an I/H section for example, because d is big and flange thickness (the h in the above formulas) is quite small. Usually in enginnereing cross sections the parallel axis term $Ad^2$ is much bigger than the centroidal term $I_o$. In the case of a rectangular section around its horizontal axis, this can be transformed into Where $\rho$ is the distance from any given point to the axis. The moment of inertia of an object around an axis is equal to You have misunderstood the parallel axis theorem.


 0 kommentar(er)
0 kommentar(er)
